Myers' Diff Algorithm in Clojure
If you’re a programmer, you’re probably fairly comfortable with
understanding and interpreting diff patches of the kind that git and
other version control systems use. In this post we’ll walk through a
Clojure implementation of the Myers’ diff algorithm, which is the
algorithm used by Git.
I have been implementing Git following along James Coglan’s book “Building Git”– you can check out the project here. The project itself is in Rust but I thought it might be an interesting exercise to implement the algorithm in Clojure.
Edit graph
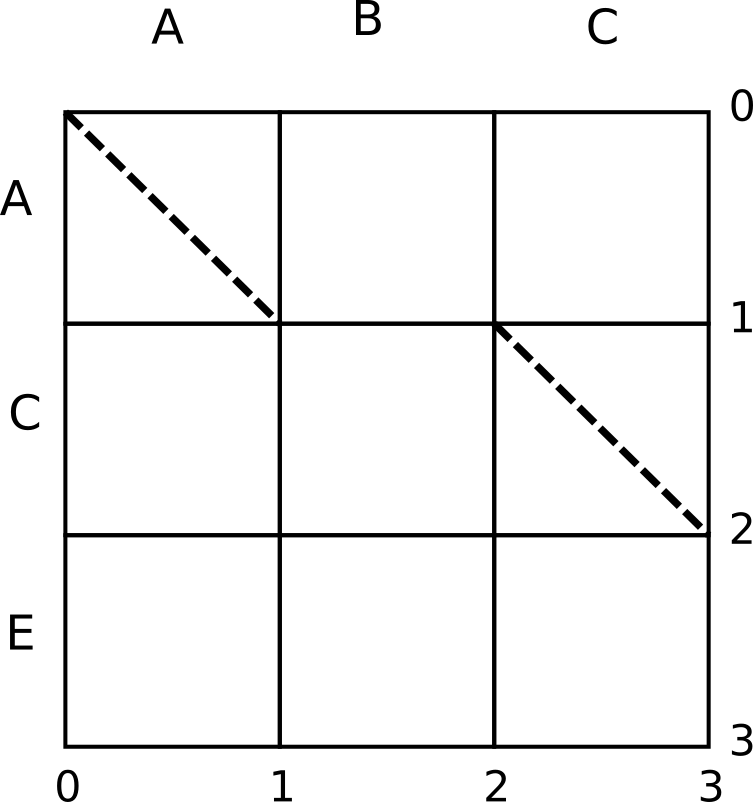
Say we want to turn a file with the lines A,B,C into A,C,E. The
Myers’ diff algorithm finds out the shortest edit script that does
so. The algorithm works on an edit graph as shown above– a rightward
traversal from one vertex to another indicates deletion of a line from
the old file; a downward traversal indicates insertion of a line from
the new file.
Also notice that in our example ABC -> ACE there are two lines which
are the same(A & C). Myers’ algorithm leverages this to produce the
shortest edit script. In our edit graph above, you can see that where
lines are equal we have drawn dotted lines to indicate diagonal
traversals which require neither insertion nor deletion. The Myers’
algorithm maximizes the number of diagonal traversals in the edit
script it produces1.
Let’s walk through the output Myers’ algorithm produces for our example above:
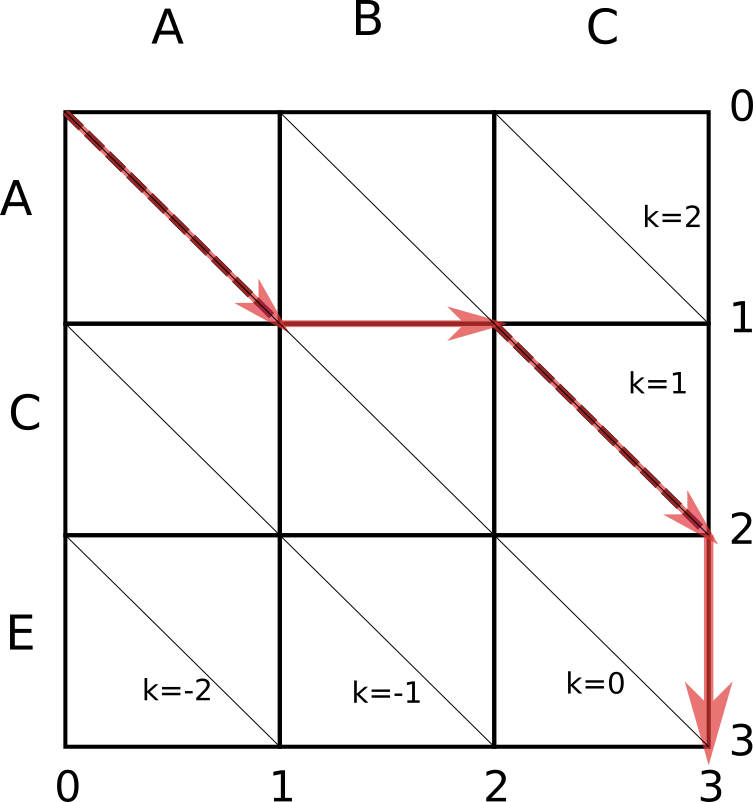
The first character is the same in both files so take the first
diagonal down. Then delete B. The third character in the old
file(C) is the same as the second in the new file so keep it and do
a diagonal traversal again. Then insert E. This series of edits on
the old file has produced our desired new file, and so we stop.
Finally, before we dive into the algorithm, we have one more addition
to the edit graph. We will draw downward-diagonals across the graph,
also called k-lines. Each k-line has the equation k = x - y.
Implementation
The maximum number of operations(insertions or deletions) the edit
script can have is len(old) + len(new)– in this case we would be
deleting every line in the old file and inserting every line from the
new file.
We iterate through 0 to maximum number of operations and see what the
farthest point along each k-line we can go. In the reduce, we can
see that our accumulator is a tuple with v and trace.
v maps each k to the farthest x we have found so far along that
k-line. We can discard the y values since we can easily compute
them(y = x - k).
trace is a vector of the vs we’ve seen so far.
We can see that the function ultimately returns trace. This will be
used to reconstruct the path that we took along the graph.
(defn shortest-edit [a b] (let [max (+ (count a) (count b)) [_ trace] (reduce (fn [[v trace] d] (let [[found-end? farthest-xs] (get-farthest-xs-for-d v a b d) [new-v new-trace] [(merge v farthest-xs) (conj trace v)]] (if found-end? (reduced [new-v new-trace]) [new-v new-trace]))) [{1 0} []] (range 0 (inc max)))] trace))
To get to a line k, we can either go down from k+1 or go right from
line k-1. We use the move-down? function to decide whether to move
down or right:
(defn move-down? [v d k] (or (= k (- d)) (and (not= k d) (< (get v (dec k)) (get v (inc k))))))
If k=-d, it is not possible to go right from k-1, so go down from k+1.
If k=d, it is not possible to go down from k+1, so go right from k-1.
Otherwise, go down if
v[k-1] < v[k+1].What this expression in the predicate is saying is: if we are further along on the k+1 line, we want to go down to meet the k line. Else go right from the k-1 line.
Next, in get-farthest-xy-along-k* we figure out what the farthest
(x,y) we can reach in this round d along the k line given the v
map we’ve built so far. a and b contain the lines that we want to
diff. This simply uses move-down?as described above; then if
possible walks down any diagonals.
(defn get-farthest-xy-along-k* [v d a b k] (let [x (if (move-down? v d k) (get v (inc k)) (inc (get v (dec k)))) y (- x k) ;; walk down diagonals [x y] (loop [[x y] [x y]] (if (and (< x (count a)) (< y (count b)) (= (get a x) (get b y))) (recur [(inc x) (inc y)]) [x y]))] [x y]))
get-farthest-xs-for-d iterates from -d to d(both inclusive), 2 steps
at a time2 and stores the farthest x for each k, returning
early if we reach the bottom-right corner in our edit graph.
(defn get-farthest-xs-for-d [v a b d] (let [get-farthest-xy-along-k (partial get-farthest-xy-along-k* v d a b)] (reduce (fn [[found-end? k->x] k] (let [[x y] (get-farthest-xy-along-k k)] (if (and (>= x (count a)) (>= y (count b))) (reduced [true k->x]) [found-end? (assoc k->x k x)]))) [false {}] (range (- d) (inc d) 2))))
So far, we’ve built up functions that give us a trace:
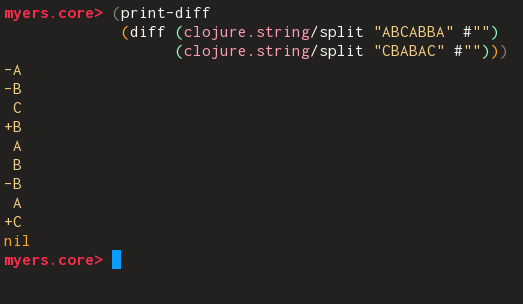
myers.core> (shortest-edit (clojure.string/split "ABCABBA" #"") (clojure.string/split "CBABAC" #"")) [{1 0} {1 0, 0 0} {1 1, 0 0, -1 0} {1 1, 0 2, -1 0, -2 2, 2 3} {1 5, 0 2, -1 4, -2 2, 2 3, -3 3, 3 5} {1 5, 0 5, -1 4, -2 4, 2 7, -3 3, 3 5, -4 3, 4 7}] myers.core>
Now, let’s look at how to turn this into a diff.
Backtracking and producing the diff
This next function will take an input a trace and output an edit
sequence. Each element in the edit-sequence is of the form [prev-x
prev-y x y].
This time we start from the bottom-right node of the edit graph. In each iteration, we figure out the previous (x,y)– also walking back up diagonals if required.
(defn trace->edit-seq [n m trace] (let [[_ edit-seq] (reduce (fn [[[x y] edit-seq] [d v]] (let [k (- x y) prev-k (if (move-down? v d k) (inc k) (dec k)) prev-x (get v prev-k) prev-y (- prev-x prev-k) [[x y] edit-seq] (loop [[x y] [x y] edit-seq edit-seq] (if (and (> x prev-x) (> y prev-y)) (recur [(dec x) (dec y)] (conj edit-seq [(dec x) (dec y) x y])) [[x y] edit-seq])) edit-seq (if (pos? d) (conj edit-seq [prev-x prev-y x y]) edit-seq)] [[prev-x prev-y] edit-seq])) [[n m] []] (reverse (map vector (range) trace)))] (reverse edit-seq)))
Once we have an edit sequence, printing the diff is pretty straightforward:
(defn diff [a b] (for [[prev-x prev-y x y] (trace->edit-seq (count a) (count b) (shortest-edit a b))] (let [a-line (get a prev-x) b-line (get b prev-y)] (cond (= x prev-x) {:op :ins :content b-line} (= y prev-y) {:op :del :content a-line} :else {:op :eql :content a-line})))) (defn print-diff [diff] (doseq [{:keys [op content]} diff] (let [d-out (case op :ins (format "+%s" content) :del (format "-%s" content) :eql (format " %s" content))] (println d-out))))
which is also why finding the shortest edit script and finding the longest common subsequence are equivalent problems.
if
dis even, you can only reach an even k-line, and vice-versa.